GEOMETRÍA 8 Y 9

Jóvenes de grado 8 y 9 I.E.C. sede Marco Fidel. A  continuación encontraran información importante para entender algunas propiedades de los triángulos, copiar toda la información correspondiente y finalmente desarrollar los 2 ejercicios propuestos, en el transcurso de los días propondremos nuevos ejercicios, recuerden que estas actividades son para desarrollar en un plazo de 15 días. A continuación se presenta un vídeo, al cual deben hacer una reflexión y entregarla vía whatsapp el día 24 de abril. Ángulos en un triángulo

Los ángulos que se forman en un triángulo se relacionan entre sí cumpliendo con las siguientes propiedades o características:

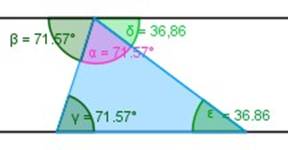
1.- La suma de los ángulos internos de un triángulo es igual a dos ángulos rectos; es decir, suman 180º. En la figura, α + γ + ε = 180º . Recordar que γ = β y que ε = δ por ser ángulos alternos internos .

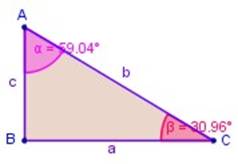
2.- La suma de los ángulos agudos de un triángulo rectángulo es igual a 90º. En la figura, α + β = 90º

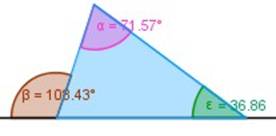
3.- En todo triángulo, la medida de un ángulo externo es igual a la suma de las medidas de los ángulos internos no contiguos (opuestos). En la figura, β = α + ε

4.- En todo triángulo la medida de un ángulo externo es mayor que la de cualquier ángulo interior no adyacente. En la figura, β > (es mayor que) α β > (es mayor que) e

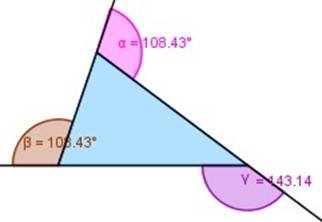
5.- La suma tres ángulos exteriores de cualquier triángulo vale cuatro ángulos rectos; es decir, suman 360º. En la figura, α + β + γ = 360º

Veamos un ejemplo

Ejercicio 1.-

En la siguiente imagen, ¿Cuál es el valor del ángulo x?
(Fig. 3)

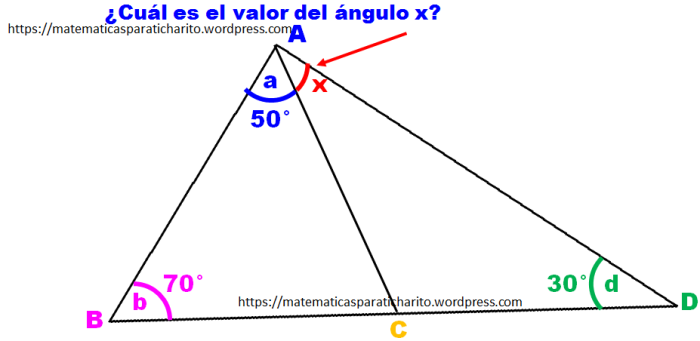
Para saber el valor de x partimos del triángulo de la izquierda, del cual conocemos la medida de dos de sus ángulos.
Sabiendo que los ángulos internos del triángulo suman 180°, el ángulo c será igual a 180 menos la suma de los ángulos b y d (Fig. 4).

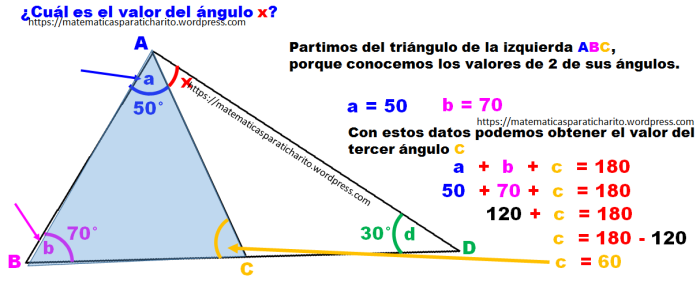
Sabiendo que c es igual a 60° y que es suplementario con el ángulo que tiene a la derecha y que pertenece al segundo triángulo, podremos obtener el valor de x.
Llamemos a este ángulo con la letra e.
Si a 180 le quito el valor de c, que es 60°, obtengo el valor del ángulo e, que es 120°
(fig: 5)

Y sabiendo este valor, conozco dos ángulos del triángulo de la derecha, d que vale 30° y e que vale 120°.
Si sumo estos valores y el resultado lo resto a 180° que es el valor de la suma de los tres ángulos internos del triángulo, obtengo el valor del tercer ángulo designado con x (Fig. 6).

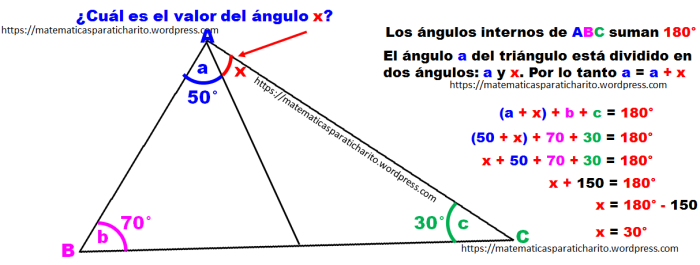
Una forma muy sencilla de obtener también el valor de “x” es la siguiente:
Los ángulos “a”, “b” y ”d” son los tres ángulos del triángulo mayor, sin considerar los dos triángulos en los que se divide. Quiere decir que “a” más “b” más “d” es igual a 180°
Observa que “a” se forma con “a” más “x”, por lo que los 180° se obtienen sumando “a” más “x” más “b” más “d”.
El valor de “x” lo obtenemos de la siguiente manera (Fig. 7)

EJERCICIOS

Resolver los siguientes triángulos, hallar para cada uno el valor correspondiente al ángulo (x)